Imagine before you made your next investment move that you knew the outcome of it in advance.

What kind of confidence and security could that provide to you as you make investment decisions?

If it seems like a fantasy, you’re going to want to keep reading, because I think you’ll be surprised.

Especially once you find out what baseball has to do with all of this…

The Moneyball of Investing

Growing up, I loved to watch and play baseball and I was an avid baseball card collector.

It wasn’t until I was in my teens that I recognized the importance of all of those statistics that are kept for each player.

Being numbers-oriented as I am and a baseball enthusiast, it was only natural I would enjoy the 2011 movie Moneyball.

The movie is based on the true story of Billy Beane (played by Brad Pitt), who was the general manager of the Oakland A’s.

In 2002, with the challenge of rebuilding the team with a limited budget, Beane meets a young Yale economic graduate who suggests that by just focusing on the stats of players, they can assemble a winning team.

Beane takes a gamble, and it works as the Athletics win the 2002 American League West title.

The method that Beane introduced to baseball has since become widely used throughout the League.

The idea that Beane put to work is the idea that a player, after so many times at bat (occurrences), becomes predictable. So by assembling a team where every player is expected to get a hit, the team will probably be overall successful.

Here is the cool thing. You can (and should) put this same concept to work in your portfolio.

Welcome to the “Moneyball of Investing” known as expectancy investing.

Expectancy is the expected profit or loss from making an investment.

It’s something EVERY investor should know PRIOR to making an investment.

Most investors do not and, as a result, are gambling, to be frank.

Think of it like a coin toss.

Every coin toss has the same predictable outcome: Heads 50%, Tails 50%.

It doesn’t matter if heads comes up for 10 consecutive tosses – each toss is independent of the prior toss and has the same predictable outcome.

Now let’s make it interesting.

Let’s say that every time you win, you get to keep $2 and every time you lose you have to pay $1.

Interested? You better be, because that’s the formula for unlimited wealth!

The outcome – your earnings from this coin toss – are 100% predictable and known in advance.

We know that the probability of a win is 50%.

We know the average win is $2, and that the average loss is $1.

The formula thus is (50% x $2) – (50% x 1) which equals $.50.

This means that for EVERY coin toss, whether you win or lose on that event, you are EXPECTING to earn $0.50 because that is the built-in expectancy.

It’s a mathematical law where the greater the number of occurrences (coin tosses), the more predictable the outcome.

Billy Beane knew that if a player had enough swings at the bat, he was going to get a hit, and it would be more than enough times to make up for the times that the player didn’t. Billy was simply using mathematical expectancy.

Theoretically, you could recreate this wonderfully positive return scenario with your real-life investment portfolio.

We all have access to the same investment products, but we’ll all produce massively different investment results.

The difference has to be the investment process since everyone has the same investment products to pick from.

If investors use a process that is based on mathematical expectancy, then the outcome of the investment should be known BEFORE having made the actual investment.

To employ this method, let’s first discuss how NOT to invest.

Most investors use an approach that is completely random. Tips, analyst reports, financial media, your second cousin Eddie, or anything similar has an unknown outcome that is no better than gambling.

Not until you invest systematically can you know the expectancy of your investment.

To invest systematically, you must use a defined set of rules that determine what you buy, when you buy, and when you sell.

Let me share some examples.

One of the most basic and easiest-to-understand systems is based on moving averages.

Let’s assume we will buy the S&P 500 SPDR (SPY) if, on the last day of the month, the price exceeded the 200-day simple moving average (SMA).

Our sell rule would be simply the opposite. We would sell SPY and move to cash if the price ended the month below the 200 SMA.

All are simple and easy to understand and implement.

Since 1999, there have been 15 occurrences where this set of rules would have applied.

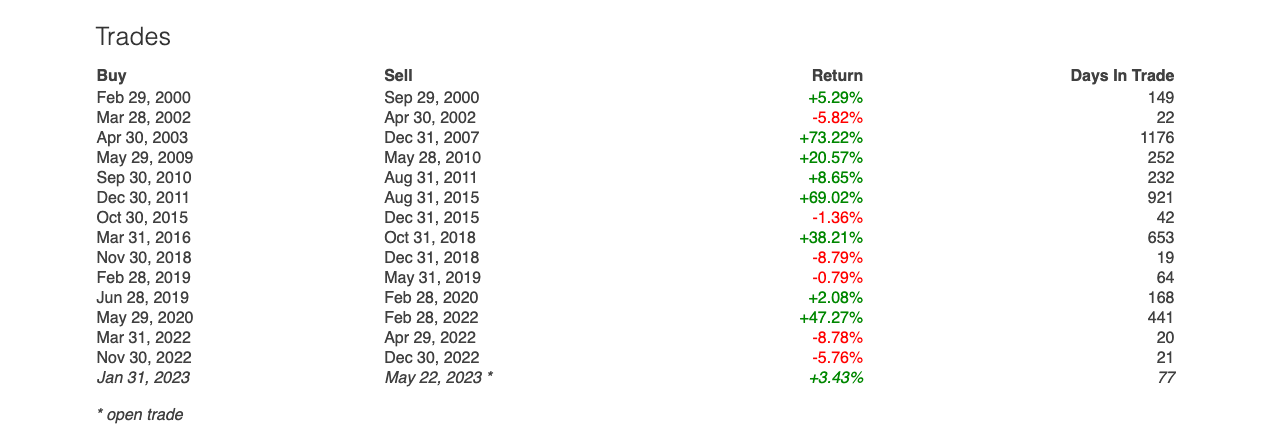
Some 60% of the trades resulted in winners with a median gain of 20.57%.

The 40% losing trades had an average loss of only -5.79%.

To determine our expectancy of using the 200-day period SMA strategy, we calculate the following:

(60% x 20.57%) – (40% x 5.79%) = 12.34 – 2.32% = 10.02%

This means we can expect to make a gain of about 10.02% for every buy signal we take.

It doesn’t mean that you will, but it means that over time, the collective gains from all signals taken should be close to our expected return.

Cumulatively, the system has returned 527.1% vs. 367.1% for buying and holding the SPY.

Additionally, by having a defined sell rule, it minimized the downside to 25.5% vs. a maximum decline of 55% for the SPY.

Not too bad, right? More return and half the risk.

We know that based on historical data, we stand a good chance of winning by following the system.

And we know this before we ever invest a nickel.

Let’s walk through another example with Avalon’s Volatility Resistant Model.

As the model is 100% systematic, we can calculate its mathematical expectancy. And since the strategy uses a monthly rebalance, we measure the result of each monthly set of securities, beginning in January 2007.

Out of 197 occurrences, the strategy produced a positive gain in 66% of those months. The average of those gains has been 2.19%.

In the 34% of those months, that resulted in a loss, the average of those losses has been -1.27%.

Using the same formula shows us that this model has a mathematical expectancy of positive 1.01% a month.

This means that an investor can expect to make this amount each month that they are invested in this model. With compounding, this works out to be about 13.5% compound annual growth.

The power of investing with mathematical expectancy is that it allows investors to reliably profit from investing when the future is unknown and the markets appear to be random.

Mathematical expectancy is how you convert an unknowable and uncertain future into statistical confidence. It’s how you convert doubt into a predictable outcome.

The advantage of using a systematic, model approach to investing is that the model processes the future data in a predictable fashion, month, after month, after month.

Here at Avalon, we believe that using systematic, rules-based models provides more predictable and reliable outcomes than any other form of investing.

To learn more about the advantages of model investing and how to put the power of mathematical expectancy to work for you, schedule your free consultation with one of our advisors today.