Growing up, I loved to watch and play baseball and I was an avid baseball card collector, but it wasn’t until I was in my teens that I recognized the importance of all of those statistics kept for each player.  

Being numbers-oriented as I am and a baseball enthusiast, it was only natural I would enjoy the 2011 movie “Moneyball.” I’m sure many readers may be familiar with this movie. The movie is based on the true story of Billy Beane (played by Brad Pitt), who was the general manager of the Oakland A’s.  

In 2002, with the challenge of rebuilding the team with a limited budget, Beane meets a young Yale economic graduate who suggests that by just focusing on the stats of players, they can assemble a winning team.  

Beane takes a gamble and it works as the Athletics win the 2002 American League West title.  

The methodology that Beane introduced to baseball has since become widely used throughout the League. The idea he put to work is that a player, after so many times at bat (occurrences), begins to become predictable.   

So by assembling a team where every player is expected to get a hit, the team will likely be overall successful.   

Here is the cool thing. You can – and should – put this same concept to work in your portfolio. 

Welcome to the “Moneyball of Investing,” also known as expectancy investing.

So, what exactly is expectancy, and why is it so important?

Expectancy is the anticipated profit or loss from making an investment. It is something EVERY investor should know PRIOR to making an investment. 

Most investors do not and, as a result, are gambling, to be frank.

To begin this discussion, let’s review the classic coin toss.

Every coin toss has the EXACT SAME PREDICTABLE OUTCOME: Heads 50%. Tails 50%.

It does not matter if heads comes up for 10 consecutive tosses. Each toss is independent of the prior toss and has the same predictable (50%) outcome.

Now let’s make it interesting.

Let’s say that every time you win, you get to keep $2. And every time you lose you have to pay $1.

Interested?

Heck yeah… you better be, because that is the formula for unlimited wealth! The more coin tosses you can call correctly, the more money you will make… over time.

The outcome, your earnings from this coin toss, are 100% predictable and known in advance.

We know that the probability of a win is 50%.

We know the average win is $2, and that the average loss is $1.

The formula thus is (50% x $2) – (50% x 1) which equals $.50.

This means that for EVERY coin toss, whether you win or lose on that particular event, you are EXPECTING to earn $0.50 because that is the built-in expectancy. It’s a mathematical law where the greater the number of occurrences (coin tosses), the more predictable the outcome.

Billy Beane knew that if a player had enough swings at the bat, he was going to get a hit, and it would be more than enough times to make up for the times that the player didn’t. Billy was simply using mathematical expectancy.   

What if you could recreate this wonderfully positive return scenario with your real-life investment portfolio?

This is nothing new. Casinos and insurance companies have built empires around this concept.

On a roulette wheel, there are 18 red bets and 18 black bets with each paying $1. This would be no better than a coin toss. But, the casino does something sneaky. In America, they add two green boxes. This one feature gives the house a 5.26% advantage.

Thus the casino knows that it’s only a matter of enough spins of the wheel for them to collect their fortune. It’s a mathematical guarantee to them!

Consider this: We all have access to the same investment products, but we’ll all produce massively different investment results. The difference has to be the investment process since everyone has the same investment products to pick from.

If investors use a process that is based upon mathematical expectancy, then the outcome of the investment should be known BEFORE having made the actual investment.

How do you do this? First, let me tell you how NOT to invest.

Most investors use an approach that is completely random. Tips, analyst reports, financial media, or anything similar have an unknown outcome that is no better than gambling. 

Not until you begin to invest systematically can you know the expectancy of your investing.

By systematically, I mean by using a defined set of rules that determine what you buy, when you buy, and when you sell.

Let me share some examples.

One of the most basic and easiest to understand systems is based upon moving averages.

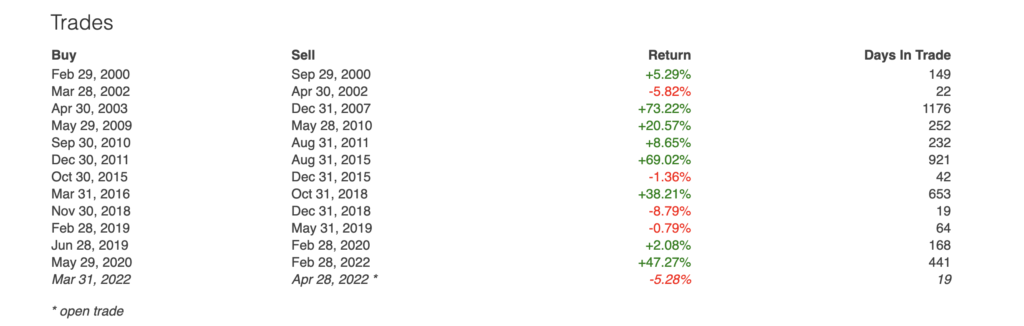
Let’s assume we will buy the S&P 500 SPDR (SPY) if on the last day of the month the price exceeded the 200-day simple moving average (SMA).

Our sell rule would be simply the opposite. We would sell SPY and move to cash if the price ended the month below the 200 SMA.

All are simple and easy to understand and implement.

Since 1999, there have been 13 occurrences where this set of rules would have applied.

Some 61.50% of the trades resulted in winners with a median gain of 29.39%.  

The 38.5% losing trades had an average loss of only -5.28%

To determine our expectancy of using the 200-day period SMA strategy, we calculate the following:

(61.5% X 29.39%) – (38.5% * 5.28%) = 18.07 – 2.03% = 16.04%.

This means we can expect to make a gain of about 16.04% for every buy signal we take.

It doesn’t mean that you will but it does mean that over a period of time, the collective gains from all signals taken should be close to our expected return.

On a cumulative basis, the system has returned 568% vs. 369.1% for buying and holding the SPY.

And in addition, by having a defined sell rule, the downside was minimized to 20.8% vs. a maximum decline of 55% for the SPY.

Not bad. More return and half the risk.

More importantly, we know that based on historical data, we stand a good chance of winning by following the system.

And we know this before we ever invest another nickel.

Trend-following systems such as this are just but one example.

I will show you another example by way of our recently introduced Volatility-Resistant Model.

Since the strategy utilizes a monthly rebalance, I will measure the result of each monthly set of securities.    

Out of 184 occurrences (swings of the bat), the strategy has produced a positive gain in 69% of those months. The average of those gains has been 2.05%.

In 31% of those months, the results were a loss, the average of those losses has been -1.30%.  

Using the same formula provided above shows us that this model has a mathematical expectancy of positive 1.01% a month.    

This means an investor can expect to make this amount each month that they are invested in this model. With compounding, this works out to be about 13.5% compound annual growth.    

The power of investing with mathematical expectancy is that it allows investors to reliably profit from investing when the future is unknown and the markets appear to be random.  

Mathematical expectancy is how you convert an unknowable and uncertain future into statistical confidence. It’s how you convert doubt into a predictable outcome.

The advantage of using a systematic, model approach to investing is that the model processes the future data in a predictable fashion, month, after month, after month.

Here at Rowe Wealth, we believe that using systematic, rules-based models provides more predictable and reliable outcomes than any other form of investing.